Soft Condensed Matter
Effective area-elasticity and tension of micro-manipulated membranes
Fluid membranes in aqueous solutions often consist of a fixed number of highly
insoluble lipid or surfactant molecules. Since stretching a flat membrane
involves very high energies, while macroscopically bending it involves
energies of order 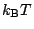 , membranes are commonly modeled as fluctuating
two-dimensional sheets with a prescribed microscopic area
, membranes are commonly modeled as fluctuating
two-dimensional sheets with a prescribed microscopic area 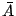 and a
curvature elasticity. At the macroscopical scale,
however, membranes appear completely different: their optically visible area
and a
curvature elasticity. At the macroscopical scale,
however, membranes appear completely different: their optically visible area 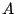 is unconstrained, and it fluctuates about some value depending on the
temperature and on the external constraints. Part of the total area
is unconstrained, and it fluctuates about some value depending on the
temperature and on the external constraints. Part of the total area 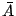 is
stored in short scale fluctuations that are optically
unresolved. For such a critically fluctuating system,
a coarse-grained effective Hamiltonian
is
stored in short scale fluctuations that are optically
unresolved. For such a critically fluctuating system,
a coarse-grained effective Hamiltonian
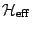 , integrating
all sub-optical details, is clearly more adequate than the microscopic
Hamiltonian.
We have evaluated this effective macroscopic Hamiltonian
, integrating
all sub-optical details, is clearly more adequate than the microscopic
Hamiltonian.
We have evaluated this effective macroscopic Hamiltonian
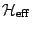 and investigated the associated area-elasticity and tension. We start
by considering a quasi-planar membrane with a fixed microscopic area
and investigated the associated area-elasticity and tension. We start
by considering a quasi-planar membrane with a fixed microscopic area 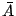 ,
which is attached to a frame of area
,
which is attached to a frame of area 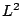 . We choose the simplest microscopic
curvature Hamiltonian: the lowest-order, quadratic approximation of the
Canham-Helfrich Hamiltonian [1,2]:
. We choose the simplest microscopic
curvature Hamiltonian: the lowest-order, quadratic approximation of the
Canham-Helfrich Hamiltonian [1,2]:
![\begin{displaymath}
{\cal H}_c[h_m]=\int\!d^2x\,\frac{\kappa}{2}\left(\nabla^2 h_m\right)^2.
\end{displaymath}](img6.gif) |
(1) |
Here 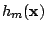 is the height of the membrane above a reference plane (Monge
gauge), as resolved microscopically. We then determine the coarse-grained
Hamiltonian
is the height of the membrane above a reference plane (Monge
gauge), as resolved microscopically. We then determine the coarse-grained
Hamiltonian
![${\cal H}_{\rm eff}[h]$](img8.gif) , where
, where 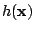 is the height of the
membrane as resolved optically. This Hamiltonian is such that
is the height of the
membrane as resolved optically. This Hamiltonian is such that
![$\exp(-\beta{\cal
H}_{\rm eff}[h])$](img10.gif) gives the probability for the occurrence of any optically
visible membrane shape
gives the probability for the occurrence of any optically
visible membrane shape 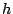 , whatever its fluctuating microscopic detail.
Technically, this is a one-step renormalization of the fixed area constraint.
We have found [3] that
, whatever its fluctuating microscopic detail.
Technically, this is a one-step renormalization of the fixed area constraint.
We have found [3] that
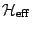 involves a
non-linear area-elasticity
energy
involves a
non-linear area-elasticity
energy 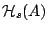 for the coarse-grained,
optically visible, area
for the coarse-grained,
optically visible, area 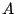 . This
is the effective potential which is probed
by pulling a membrane in an optically
resolved micro-manipulation. Depending
on the microscopic excess area
. This
is the effective potential which is probed
by pulling a membrane in an optically
resolved micro-manipulation. Depending
on the microscopic excess area
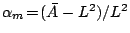 and on the
constraints exerted on the membrane,
we find three distinct regimes: a floppy
regime, an entropic-tense regime, and a
stretched-tense regime. We have
provided explicit formulae for the effective tension
and on the
constraints exerted on the membrane,
we find three distinct regimes: a floppy
regime, an entropic-tense regime, and a
stretched-tense regime. We have
provided explicit formulae for the effective tension
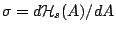 in these three regimes.
in these three regimes.
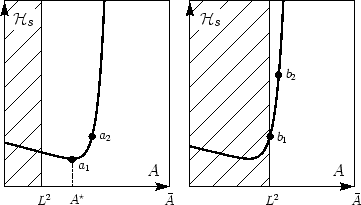
Figure 1:
Coarse-grained area-elasticity 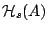 as a function of the
apparent area
as a function of the
apparent area 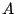 . Since
. Since 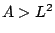 , the hatched region is physically unaccessible.
Depending on the microscopic excess area, the membrane is initially floppy
(
, the hatched region is physically unaccessible.
Depending on the microscopic excess area, the membrane is initially floppy
(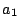 ) or tense (
) or tense (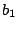 ). Further stretching can be externally induced
(
). Further stretching can be externally induced
(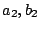 ). The floppy membrane (
). The floppy membrane (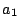 ) can, e.g., be led into a state of
tension (
) can, e.g., be led into a state of
tension (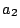 ) similar to that of the unperturbed tense one (
) similar to that of the unperturbed tense one (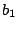 ).
).
 |
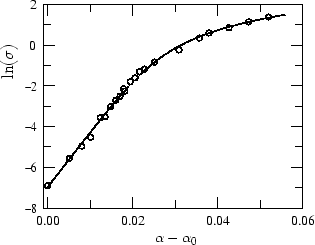
Our results can be applied to giant vesicles.
This
allows us to perform a first test of our theory: re-analyzing the
micro-pipette experiments of Evans and Rawicz [4,5], we
find
an excellent fit for the cross-over between the entropic-tense and the
stretched-tense regimes.
Figure 2:
Fit of the data obtained in a recent
micropipette experiment by Evans et al. [5].
 |
- 1
- P. Canham, J. Theor. Biol. 26, 61 (1970).
- 2
- W. Helfrich, Z. Naturforsch. 28C, 693 (1973).
- 3
- J.-B. Fournier, A. Ajdari and L. Peliti, Phys. Rev. Lett.
86, 4970(2001).
- 4
- E. Evans and W. Rawicz, Phys. Rev. Lett. 64, 2094 (1990).
- 5
- W. Rawicz et al., Biophys. J. 79, 328 (2000).
 Back to Soft Condensed Matter
Back to Soft Condensed Matter
![]() , membranes are commonly modeled as fluctuating
two-dimensional sheets with a prescribed microscopic area
, membranes are commonly modeled as fluctuating
two-dimensional sheets with a prescribed microscopic area ![]() and a
curvature elasticity. At the macroscopical scale,
however, membranes appear completely different: their optically visible area
and a
curvature elasticity. At the macroscopical scale,
however, membranes appear completely different: their optically visible area ![]() is unconstrained, and it fluctuates about some value depending on the
temperature and on the external constraints. Part of the total area
is unconstrained, and it fluctuates about some value depending on the
temperature and on the external constraints. Part of the total area ![]() is
stored in short scale fluctuations that are optically
unresolved. For such a critically fluctuating system,
a coarse-grained effective Hamiltonian
is
stored in short scale fluctuations that are optically
unresolved. For such a critically fluctuating system,
a coarse-grained effective Hamiltonian
![]() , integrating
all sub-optical details, is clearly more adequate than the microscopic
Hamiltonian.
We have evaluated this effective macroscopic Hamiltonian
, integrating
all sub-optical details, is clearly more adequate than the microscopic
Hamiltonian.
We have evaluated this effective macroscopic Hamiltonian
![]() and investigated the associated area-elasticity and tension. We start
by considering a quasi-planar membrane with a fixed microscopic area
and investigated the associated area-elasticity and tension. We start
by considering a quasi-planar membrane with a fixed microscopic area ![]() ,
which is attached to a frame of area
,
which is attached to a frame of area ![]() . We choose the simplest microscopic
curvature Hamiltonian: the lowest-order, quadratic approximation of the
Canham-Helfrich Hamiltonian [1,2]:
. We choose the simplest microscopic
curvature Hamiltonian: the lowest-order, quadratic approximation of the
Canham-Helfrich Hamiltonian [1,2]:
