Soft Condensed Matter

Why is the DNA denaturation transition first order?

Thermal denaturation or melting of double-stranded DNA is the process by which the two strands unbind upon heating. The nature of this transition has been investigated for almost four decades. Experimentally, the transition from bound to unbound is first order.

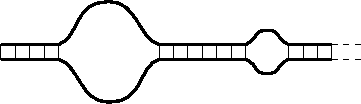
The early theoretical models [1], which we refer to as Poland-Scheraga (PS) type models, consider the DNA molecule as composed of an alternating sequence of bound and denaturated states (see, e.g., Fig. 1) Typically a bound state is energetically favored over an unbound one, while a denaturated segment (loop) is entropically favored over a bound one. Within the PS type models the segments which compose the chain are assumed to be non-interacting with one another. This assumption considerably simplifies the theoretical treatment and enables one to calculate the resulting free energy. In the past the entropy of the denaturated loops has been evaluated by modelling them either as ideal random walks [2] or as self-avoiding walks [3]. It has been found that within this approach the denaturation transition of DNA is continuous both in two and three dimensions. It becomes first order only above four dimensions.

Figure 1: Schematic representation of the Poland-Scheraga model.

We have considered analytically the effects of excluded-volume interaction between the various segments of the chain [4]. Although we treated this interaction only in an approximate way, we were able to give some insight into the unbinding mechanism and on the nature of the transition. Our approach makes use of recent important results on the entropy of self-avoiding polymer networks [5,6]. We find that this interaction drives the transition first order in $d=2$, 3 and $4-\varepsilon$ dimensions.

The PS model considers two strands, made of monomers, each representing one persistence length of a single strand ($\sim 40$ Å). A typical DNA configuration is shown in Fig. 1. It is made of sequences of bound monomers separated by denaturated loops. The statistical weight of a bound sequence of length $k$ is $\omega^k = \exp(-kE_0/T)$, where $T$ is the temperature. On the other hand the statistical weight of a denaturated sequence of length $k$ is given by the change in entropy due to the added configurations arising from a loop of length $2k$. For large $k$ this has the general form $A s^k/k^c$, where $s$ is a non-universal constant and the exponent $c$ is determined by the properties of the loop configurations. For simplicity, we set $A=1$. The model is most easily studied within the grand canonical ensemble where the total chain length $L$ is allowed to fluctuate. The grand canonical partition function, ${\cal Z}$, is given by

$${\cal Z}= \sum_{M=0}^{\infty}G(M)z^M=\frac{V_0(z)U_L(z)}{1-U(z)V(z)},$$ (1)

where $G(M)$ is the canonical partition function of a chain of length $M$, $z$ is the fugacity and

$$U(z)=\sum_{k=1}^{\infty}\frac{s^k}{k^c}z^k, \qquad V(z)=\sum_{k=1}^{\infty}\omega^k z^k,$$ (2)

$V_0(z)=1+V(z)$ and $U_L(z)=1+U(z)$. In the thermodynamic limit, $L\to \infty$, one has

$$\ln {\cal Z} \simeq L \ln z^*.$$ (3)

Here $z^*$ is the value of the fugacity in the limit $\langle L \rangle \to \infty$. This is the lowest value of the fugacity for which the partition function (1) diverges, i.e., for which $U(z^*)V(z^*)=1$.

It is thus clear that the nature of the denaturation transition is determined by the dependence of $z^*$ on $\omega$. The transition takes place when $z^*$ reaches $1/s$. Its nature is determined by the behaviour of $U(z)$ in the vicinity of $z_{\rm c}$. This is controlled in turn by the value of the exponent $c$. There are three regimes:

1. For $c\le 1$, $U(z_c)$ diverges, so that $z^*$ is an analytic function of $\omega$ and no phase transition takes place.
2. For $1<c\le 2$, $U(z_c)$ converges but its derivative $U'(z)$ diverges at $z^*=z_c$. Thus the transition is continuous.
3. For $c>2$, both $U(z)$ and its derivative converge at $z^*=z_c$ and the transition is first order. Here, in contrast to the continuous case, the average size of a denaturated loop is finite at the transition.

The value of the exponent $c$ can be obtained by enumerating random walks which return to the origin, so that $c=d \nu$. For ideal random walks this yields $c=d/2$: thus there is no transition at $d\le 2$, a continuous transition for $2<d \le 4$ and a first order transition only for $d>4$ [2]. On the other hand, for self-avoiding random walks the excluded volume interaction modifies the exponent to $c=3/2$ for $d=2$ and $c\simeq 9/5$ for $d=3$ (we use the Flory values of the exponents). The transition is thus sharper, but still continuous, in three dimensions [3].

In the above treatment the entropy of a loop of length $2l$ was taken to be of the form $s^l/l^c$. In order to evaluate the exponent $c$ for our configuration, we use the results obtained by Duplantier et al.[5,6] for the entropy of general polymer networks. Applying these results to the relevant topology to the problem discussed in this work (Fig. 2), we obtain the appropriate value of effective exponent $c$:

$$c = \cases{ 2+13/32,& in $d=2$;\cr {} 2+\varepsilon/8+ 5 \va... ...^2/256 + \mathrm{o}(\varepsilon^2), & in $d=4 -\varepsilon$.}$$ (4)

In $d=3$ one may use Padé and Padé-Borel approximations to obtain $\sigma_3 \approx 0.18$ [6] with the value $\nu \approx 0.588$ [6] yielding $c \approx 2.1$.

The exponent $c$ is therefore larger than $2$ in both $d=2$ and $d=4-\varepsilon$, implying that in these cases the transition from native to denaturated DNA is first order. This strongly suggests that the transition is also first-order in $d=3$. This is supported by the Padé and Padé-Borel approximations in d=3.

Figure 2: The topology of the loop embedded in a chain. The distance along the chain from a vertex of type $V1$ to the nearest vertex of type $V3$ is given by $L$. The distance between the vertices of type $V3$ is equal to $l$.

1

For a review see D. Poland and H. A. Scheraga (eds.), Theory of Helix-Coil Transitions in Biopolymers (Academic, New York, 1970); F. W. Wiegel, in C. Domb and J. L. Lebowitz (eds.): Phase Transitions and Critical Phenomena Vol. 7, Pg. 101 (Academic, New York, 1983).

2

D. Poland and H. A. Scheraga, J. Chem. Phys. 45, 1456 (1966); J. Chem. Phys. 45, 1464 (1966).

3

M. E. Fisher, J. Chem. Phys. 45, 1469 (1966).

4

Y. Kafri, D. Mukamel, and L. Peliti, Phys. Rev. Lett. 85, 4988 (2000).

5

B. Duplantier, J. Stat. Phys. 54, 581 (1989).

6

L. Schäfer, C. von Ferber, U. Lehr and B. Duplantier, Nucl. Phys. B 374, 473 (1992).

Back to Soft Condensed Matter