Slow dynamics and aging

We do not usually worry about the age of a
physical system: a Helium atom which was formed in the Big Bang cannot be
distinguished from one synthesized in the Sun a few days ago. However, we do
know that some everyday materials, like plastics, change their properties with
age: older samples are less resilient than younger ones when a steady tension is
applied to them. It is remarkable that the difference only becomes apparent if
one waits long enough: experiments of short duration are unable to distinguish
between samples of different age [1]. This distinguishes physical
aging from mere metastability, in which the ``equilibrium'' properties of
the sample change with time. A subtle consequence of physical aging was noticed
some time ago by L. F. Cugliandolo and J. Kurchan [2]. At
equilibrium, there is a universal relation between the linear response function
of any observable O, 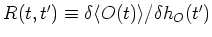 , and the corresponding correlation
function
, and the corresponding correlation
function 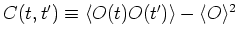 :
:
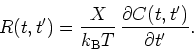 |
(1) |
The factor X is equal to 1 at equilibrium, but turns out to depend
only on C(t,t') (in a suitable long-time limit) for a class
of solvable models of aging systems, which encompasses mean-field models of spin
glasses and schematic models of structural glasses. In all these models,
X appears to be smaller than 1. The form of eq. (1) suggests to
interpret 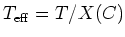 as an effective temperature: indeed, it was shown in ref. [3] that a
thermometric thought experiment would yield a temperature equal to
as an effective temperature: indeed, it was shown in ref. [3] that a
thermometric thought experiment would yield a temperature equal to 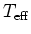 , provided that the response time of the thermometer is such that the
value of correlation function C(t,t') is equal to C
on that time scale. The details of the thermometric process have been analyzed
further in refs. [4,5] in two exactly solvable models. A very simple
lattice-gas model with kinetic constraints exhibits aging properties which can
be investigated by mean-field arguments [6]. If one modifies the evolution
of the system by a small non-conservative perturbation, aging effects disappear
in general and the system reaches a steady non-equilibrium state. However, even
in this state, the aging form of the relation (1) between response and
fluctuation remains true, as shown in Fig. 1. Therefore the introduction of
a small non-conservative perturbation is a powerful heuristic method to
investigate the aging properties of complex systems, and has been applied [7] to
the behavior of manifolds in random potentials. These researches have shown a
remarkably universal phenomenology of aging, and have lead to intriguing
predictions--like the possibility of measuring effective temperatures higher
than the ambient one in aging systems--which are currently under active
experimental investigation.
More recent investigations [8,9] have shown the intimate and quite general
relationship between the factor X which describes the violation of the
fluctuation-dissipation relation in aging and driven systems, and the functional
order parameter q(x) which describes replica-symmetry breaking
in the static properties of disordered systems and spin glasses.
, provided that the response time of the thermometer is such that the
value of correlation function C(t,t') is equal to C
on that time scale. The details of the thermometric process have been analyzed
further in refs. [4,5] in two exactly solvable models. A very simple
lattice-gas model with kinetic constraints exhibits aging properties which can
be investigated by mean-field arguments [6]. If one modifies the evolution
of the system by a small non-conservative perturbation, aging effects disappear
in general and the system reaches a steady non-equilibrium state. However, even
in this state, the aging form of the relation (1) between response and
fluctuation remains true, as shown in Fig. 1. Therefore the introduction of
a small non-conservative perturbation is a powerful heuristic method to
investigate the aging properties of complex systems, and has been applied [7] to
the behavior of manifolds in random potentials. These researches have shown a
remarkably universal phenomenology of aging, and have lead to intriguing
predictions--like the possibility of measuring effective temperatures higher
than the ambient one in aging systems--which are currently under active
experimental investigation.
More recent investigations [8,9] have shown the intimate and quite general
relationship between the factor X which describes the violation of the
fluctuation-dissipation relation in aging and driven systems, and the functional
order parameter q(x) which describes replica-symmetry breaking
in the static properties of disordered systems and spin glasses.
Figure: Top: Integrated response 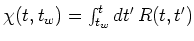 vs. the correlation function
C(t,tw) for different values of
tw in a schematic model of a structural glass.
Bottom: The corresponding plot in the presence of a nonconservative
perturbation. Different lines correspond to different intensities of the
perturbation. At equilibrium one observes a single straight line of slope
vs. the correlation function
C(t,tw) for different values of
tw in a schematic model of a structural glass.
Bottom: The corresponding plot in the presence of a nonconservative
perturbation. Different lines correspond to different intensities of the
perturbation. At equilibrium one observes a single straight line of slope 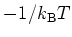 . From ref. [3].
. From ref. [3].
![\includegraphics[width=7cm]{p3chitfinite.ps}](C4_file/img8.png)
![\includegraphics[width=7cm]{p3chialpha.ps}](C4_file/img9.png)
|
Figure 2: Scheme of a thought experiment for
measuring effective temperatures in an aging magnetic system. The coil is
wound around the sample, which is in contact with the heat bath. Coil and
capacitor have zero resistance. From ref. [3].
![\includegraphics[width=6cm]{dibu.ps}](C4_file/img11.png)
|
[1] L. C. E. Struik, Physical Aging in Amorphous Polymers and
Other Materials (Elsevier, Houston, 1978).
[2] See, e.g., L. F.
Cugliandolo and J. Kurchan, Physica A 263, 242 (1999).
[3]
L. F. Cugliandolo, J. Kurchan and L. Peliti, Phys. Rev. E55,
3898 (1997).
[4] R. Exartier and L. Peliti, Physics Letters A
261, 94 (1999).
[5] R. Exartier and L. Peliti, Eur. Phys. J.
B 16, 119 (2000).
[6] L. Peliti and M. Sellitto, J. Phys.
France IV 8, Pr6, 49 (1998).
[7] P. Le Doussal, L. F.
Cugliandolo and L. Peliti, Europhys. Lett. 39, 111 (1997).
[8] S. Franz, M. Mézard, G. Parisi and L. Peliti, Phys. Rev. Lett. 81, 1758 (1998).
[9] S. Franz, M. Mézard, G. Parisi and L. Peliti, J. Stat. Phys. 97, 459 (1999).
 Back to Research Interests
Back to Research Interests


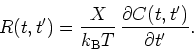
![\includegraphics[width=7cm]{p3chitfinite.ps}](C4_file/img8.png)
![\includegraphics[width=7cm]{p3chialpha.ps}](C4_file/img9.png)
![\includegraphics[width=6cm]{dibu.ps}](C4_file/img11.png)
 Back to Research Interests
Back to Research Interests